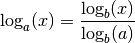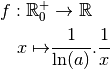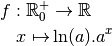4 Fonctions logarithmes¶
4.1 Définition¶
Comme les fonctions  sont des
fonctions strictement monotones et continues de
sont des
fonctions strictement monotones et continues de 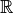 dans
dans
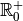 pour tout
pour tout
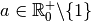 , le théorème de la
bijection (théorème 3.2.7) et les propositions
3.2.4et 3.2.5 nous assurent qu’il
existe une unique fonction réciproque définie sur
, le théorème de la
bijection (théorème 3.2.7) et les propositions
3.2.4et 3.2.5 nous assurent qu’il
existe une unique fonction réciproque définie sur
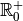 à chacune de ces fonctions :
à chacune de ces fonctions :
Définition 4.1.1 Soit 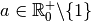 .
La fonction logarithme de base
.
La fonction logarithme de base  , notée
, notée 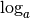 ,
est la fonction réciproque de la fonction exponentielle de base
,
est la fonction réciproque de la fonction exponentielle de base
 .
.
Remarque 4.1.2 Pour 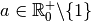 , la fonction
exponentielle de base
, la fonction
exponentielle de base  a comme domaine
a comme domaine 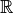 et
comme image
et
comme image 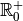 . La fonction logarithme de base
. La fonction logarithme de base
 a donc comme domaine
a donc comme domaine 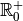 et comme
image
et comme
image 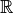 .
.
Remarque 4.1.3 Pour 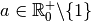 , par définition
de la fonction logarithme de base
, par définition
de la fonction logarithme de base  comme réciproque de la
fonction exponentielle de base
comme réciproque de la
fonction exponentielle de base  , on a :
, on a :
Pour tout
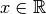 :
: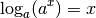
Pour tout
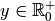 :
: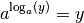
Ces simples égalités, qui caractérisent les fonctions logarithmes, sont très utiles lorsqu’on souhaite par exemple utiliser des fonctions logarithmes pour résoudre des équations.
Exemple 4.1.4 Intéressons-nous un instant à la fonction
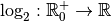 pour bien
comprendre ce que sont les fonctions logarithmes.
pour bien
comprendre ce que sont les fonctions logarithmes.
Que vaut par exemple 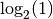 ? Puisque la fonction
? Puisque la fonction
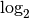 est la réciproque de la fonction
est la réciproque de la fonction 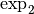 , le
nombre
, le
nombre 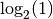 est le nombre réel
est le nombre réel
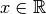 tel que
tel que  . Nous
connaissons ce nombre, il s’agit de
. Nous
connaissons ce nombre, il s’agit de  car
car 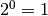 ! En
conclusion :
! En
conclusion : 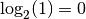 . Autre exemple : que vaut par
exemple
. Autre exemple : que vaut par
exemple  ? Puisque la fonction
? Puisque la fonction 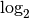 est la réciproque de la fonction
est la réciproque de la fonction 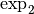 , le nombre
, le nombre
 est le nombre réel
est le nombre réel 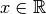 tel
que
tel
que 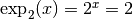 . Nous connaissons ce nombre, il
s’agit de
. Nous connaissons ce nombre, il
s’agit de  car
car 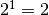 ! En conclusion :
! En conclusion :
 .
.
Un dernier exemple : que vaut par exemple 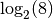 ?
Puisque la fonction
?
Puisque la fonction 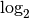 est la réciproque de la fonction
est la réciproque de la fonction
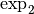 , le nombre
, le nombre 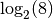 est le nombre réel
est le nombre réel
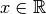 tel que
tel que 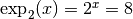 . Nous
connaissons ce nombre, il s’agit de
. Nous
connaissons ce nombre, il s’agit de 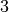 car
car 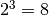 ! En
conclusion :
! En
conclusion : 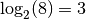 .
Bref, le logarithme de base
.
Bref, le logarithme de base 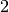 d’un nombre strictement positif
est l’unique nombre
d’un nombre strictement positif
est l’unique nombre 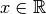 tel que
tel que
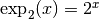 est égal à ce nombre de départ.
Plus généralement, le logarithme de base
est égal à ce nombre de départ.
Plus généralement, le logarithme de base  (pour
(pour
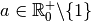 ) d’un nombre est
l’unique nombre
) d’un nombre est
l’unique nombre 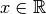 tel que
tel que
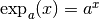 est égal à ce nombre de départ.
est égal à ce nombre de départ.
Remarque 4.1.5 Pour 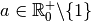 , puisque la
fonction
, puisque la
fonction 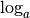 est définie comme la fonction réciproque de
la fonction
est définie comme la fonction réciproque de
la fonction 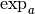 , le graphe de la fonction
, le graphe de la fonction
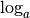 est le symétrique du graphe de la fonction
est le symétrique du graphe de la fonction
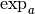 par la droite d’équation cartésienne
par la droite d’équation cartésienne 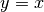 .
Par exemple, voici le graphe de la fonction
.
Par exemple, voici le graphe de la fonction 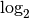 :
:
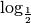 :
: )
correspond le cas exceptionnel du logarithme népérien :
)
correspond le cas exceptionnel du logarithme népérien :Définition 4.1.6. La fonction logarithme népérien 1, notée 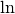 , est la
fonction logarithme de base
, est la
fonction logarithme de base  , autrement dit la fonction
, autrement dit la fonction
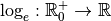 .
.
Tout comme la fonction exponentielle (de base  ) est reine parmi
les fonctions exponentielles, le logarithme népérien est roi parmi les
fonctions logarithmes. Nous découvrirons ce que le logarithme népérien a
de si particulier dans la section 4.3.
) est reine parmi
les fonctions exponentielles, le logarithme népérien est roi parmi les
fonctions logarithmes. Nous découvrirons ce que le logarithme népérien a
de si particulier dans la section 4.3.
Remarque 4.1.7. Certaines personnes notent simplement 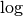 pour la fonction
logarithme en base
pour la fonction
logarithme en base 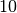 . D’autres personnes (moins nombreuses)
notent simplement
. D’autres personnes (moins nombreuses)
notent simplement 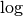 pour le logarithme en base
pour le logarithme en base 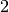 .
Dans ce cours, nous n’utiliserons aucune de ces deux notations (et je
vous conseille de faire de même).
.
Dans ce cours, nous n’utiliserons aucune de ces deux notations (et je
vous conseille de faire de même).
4.2 Propriétés élémentaires¶
Nous avions listé les propriétés des fonctions exponentielles, faisons de même pour les fonctions logarithmes.
Proposition 4.2.1. Soit 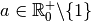 .
Le domaine de définition de la fonction
.
Le domaine de définition de la fonction 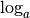 est
est
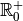 .
.
Démonstration Par définition de la fonction 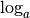 comme réciproque de la
fonction
comme réciproque de la
fonction 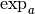 .
.
Proposition 4.2.2. Soit 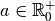 .
Si
.
Si  , l’image de la fonction
, l’image de la fonction 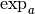 est
est
 .
Si
.
Si 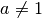 , l’image de la fonction
, l’image de la fonction 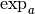 est
est
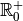 .
.
Démonstration Par définition de la fonction 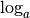 comme réciproque de la
fonction
comme réciproque de la
fonction 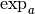 .
.
Proposition 4.2.3. Soit 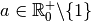 .
Si
.
Si  , la fonction
, la fonction 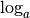 est strictement
décroissante.
Si
est strictement
décroissante.
Si  , la fonction
, la fonction 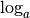 est strictement
croissante.
est strictement
croissante.
Démonstration Soient 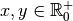 avec
avec  . Puisque
. Puisque
 , on sait que
, on sait que 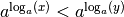 .
Deux possibilités :
.
Deux possibilités :
Si
 , comme la fonction
, comme la fonction  est une bijection
strictement décroissante, cela implique que
est une bijection
strictement décroissante, cela implique que
 . La fonction
. La fonction 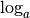 est donc bien strictement décroissante.
est donc bien strictement décroissante.Si
 , comme la fonction
, comme la fonction  est une bijection
strictement croissante, cela implique que
est une bijection
strictement croissante, cela implique que
 . La fonction
. La fonction 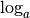 est
donc bien strictement croissante.
est
donc bien strictement croissante.
Proposition 4.2.4. Soit 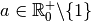 .
La fonction
.
La fonction 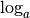 est continue.
est continue.
Démonstration Par le théorème 3.2.7, puisque la fonction
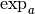 est une fonction strictement monotone continue définie
sur un intervalle, c’est une bijection et sa fonction réciproque,
c’est-à-dire la fonction
est une fonction strictement monotone continue définie
sur un intervalle, c’est une bijection et sa fonction réciproque,
c’est-à-dire la fonction 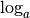 , est nécessairement continue.
, est nécessairement continue.
La limite en un point 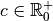 d’une fonction
logarithme est donc toujours égale à son image en ce point. Par
ailleurs, on a :
d’une fonction
logarithme est donc toujours égale à son image en ce point. Par
ailleurs, on a :
Proposition 4.2.5. Soit 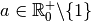 .
Si
.
Si  , on a
, on a
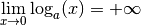 et
et
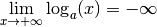 .
Si
.
Si  , on a
, on a
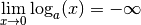 et
et
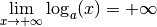 .
.
Démonstration Découle directement de la définition des fonctions logarithmes et de la proposition 2.2.7.
Vient à présent un des résultats les plus importants au sujet des fonctions logarithmes. Celui-ci est l’équivalent de la proposition 2.2.8 des fonctions exponentielles.
Proposition 4.2.6. Soient  .
.
Pour tout
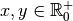 , on a :
, on a :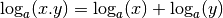
Pour tout
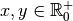 , on a :
, on a :
Pour tout
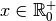 et pour tout
et pour tout
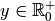 , on a :
, on a :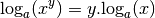
Démonstration
Pour tout
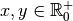 , comme la fonction
logarithme en base
, comme la fonction
logarithme en base  est la réciproque de la fonction
exponentielle de base
est la réciproque de la fonction
exponentielle de base  , par la proposition
2.2.8 :
, par la proposition
2.2.8 :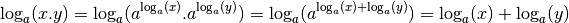
Pour tout
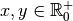 , comme la fonction
logarithme en base
, comme la fonction
logarithme en base  est la réciproque de la fonction
exponentielle de base
est la réciproque de la fonction
exponentielle de base  , par la proposition
2.2.8 :
, par la proposition
2.2.8 :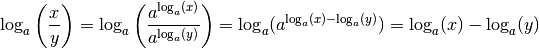
Pour tout
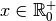 et pour tout
et pour tout
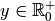 , , comme la fonction logarithme en
base
, , comme la fonction logarithme en
base  est la réciproque de la fonction exponentielle de base
est la réciproque de la fonction exponentielle de base
 , par la proposition 2.2.8 :
, par la proposition 2.2.8 :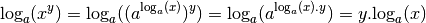
Remarque 4.2.7. De la même manière que la proposition 2.2.8 caractérisait les fonctions exponentielles, cette dernière proposition caractérise les fonctions logarithmes, en particulier la première formule. Les fonctions logarithmes sont des fonctions qui permettent de transformer des produits en sommes (c’est d’ailleurs précisément la raison pour laquelle ils ont été inventés à la base).
4.3 Dérivées des fonctions exponentielles et logarithmes¶
Les fonctions logarithmes sont continues, mais sont-elles dérivables ? Commençons avec une seule d’entre elle : le logarithme népérien.
Proposition 4.3.1. La fonction 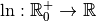 est
dérivable et sa dérivée est la fonction :
est
dérivable et sa dérivée est la fonction :

*Démonstration *Par le théorème 3.2.7, comme la fonction
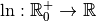 est la réciproque de la
fonction exponentielle de base
est la réciproque de la
fonction exponentielle de base  qui est dérivable et dont la
dérivée ne s’annule jamais, elle est dérivable. De plus, on sait qu’on a
pour tout
qui est dérivable et dont la
dérivée ne s’annule jamais, elle est dérivable. De plus, on sait qu’on a
pour tout 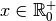 :
:
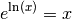
Si la fonction du membre de gauche de l’équation est égale à la fonction
du membre de droite de l’équation, alors la dérivée de la fonction du
membre de gauche de l’équation doit être égale est à la dérivée de la
fonction du membre de droite de l’équation. On doit avoir pour tout
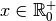 :
:
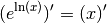
Comme la dérivée de la fonction exponentielle est elle-même, par la formule de la dérivée de la composée de deux fonctions dérivables :
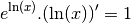
Comme pour tout 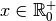 ,
,
 , on a donc pour tout
, on a donc pour tout
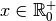 :
:
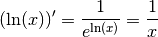
Remarque 4.3.2. Nous avons donc finalement trouvé une primitive de la fonction inverse
(sur 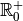 ) ! Il s’agit de la fonction
) ! Il s’agit de la fonction
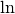 ! Nous sommes donc à présent capables de trouver une
primitive pour chaque fonction de référence.
! Nous sommes donc à présent capables de trouver une
primitive pour chaque fonction de référence.
Pour étudier la dérivabilité des autres fonctions logarithmes, nous aurons besoin de l’extrêmement utile résultat suivant :
Proposition 4.3.3. (Formule de changement de base pour les logarithmes)
Soit
. Alors pour tout
on a :
Démonstration Soit 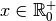 . On a :
. On a :
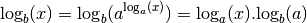
Comme 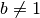 ,
, 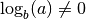 et donc :
et donc :

Remarque 4.3.4 La formule du changement de base permet par exemple de calculer un
logarithme dans une base choisie avec n’importe quel calculatrice
scientifique. En effet, si on souhaite par exemple calculer une
approximation de  mais que la calculatrice ne
propose pas la fonction
mais que la calculatrice ne
propose pas la fonction  , il suffit de calculer
, il suffit de calculer
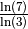 .
.
Proposition 4.3.5 Soit 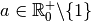 .
.
La fonction
est dérivable et sa dérivée est la fonction :
Démonstration Par la formule du changement de base, on a pour tout
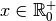 :
:
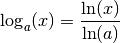
La fonction 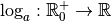 est
donc dérivable et par linéarité de la dérivée, on a pour tout
est
donc dérivable et par linéarité de la dérivée, on a pour tout
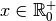 :
:
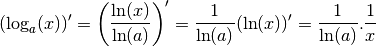
Finalement, nous sommes capables de montrer que toutes les fonctions exponentielles sont dérivables et de calculer leurs dérivées:
Proposition 4.3.6 Soit 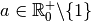 .
.
La fonction
est dérivable et sa dérivée est la fonction :
Démonstration Par le théorème 3.2.7, comme la fonction
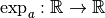 est la réciproque de la
fonction logarithme de base
est la réciproque de la
fonction logarithme de base  qui est dérivable et dont la
dérivée ne s’annule jamais, elle est dérivable. De plus, on sait qu’on a
pour tout
qui est dérivable et dont la
dérivée ne s’annule jamais, elle est dérivable. De plus, on sait qu’on a
pour tout 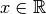 :
:
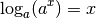
Si la fonction du membre de gauche de l’équation est égale à la fonction
du membre de droite de l’équation, alors la dérivée de la fonction du
membre de gauche de l’équation doit être égale est à la dérivée de la
fonction du membre de droite de l’équation. On doit avoir pour tout
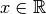 :
:
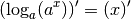
Par la formule de la dérivée de la composée de deux fonctions dérivables :
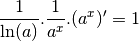
On a donc pour tout 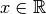 :
:
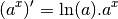
4.4 Exercices¶
Exercice 4.4.1. En utilisant les propriétés élémentaires des fonctions logarithmes, calculer les nombres suivants sans avoir recours à une calculatrice.




Exercice 4.4.2. En utilisant une calculatrice et la formule de changement de base pour
les logarithmes, trouver une approximation des nombres suivants à
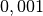 près.
près.




Exercice 4.4.3 Donner les domaines de définition réels maximaux pour les fonctions dont les expressions sont les suivantes :



Exercice 4.4.4.

Exercice 4.4.5. Pour les fonctions suivantes, déterminer si elles convergent ou
divergent pour  et
et 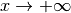 .
.








Exercice 4.4.6. Calculer les dérivées des fonctions dérivables suivantes.








Exercice 4.4.7.

Exercice 4.4.8. et Exercice 4.4.9.

Exercice 4.4.10.

Exercice 4.4.11.

Exercice 4.4.12. Calculer les intégrales des fonctions intégrables suivantes.








Exercice 4.4.13. En utilisant les propriétés des fonctions exponentielles et
logarithmes, résoudre les équations suivantes dans 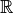 .
.








Exercices supplémentaires : https://fr.wikiversity.org/wiki/Fonction_logarithme/Exercices/%C3%89quations_comportant_des_exponentielles
Remarque 4.4.14. Il n’y a pas d’inéquation avec des fonctions logarithmes au programme du cours de mathématiques de 4 heures par semaine. Néanmoins, il est possible que vous ayez à résoudre une telle inéquation ultérieurement, par exemple dans un cours de physique. Si vous souhaitez vous entraîner, prenez les équations de l’exercice [équaloga] et remplacez les égalités par des inégalités.
Défi 4.4.15. Sans utiliser de calculatrice, déterminer si  ou
ou  ou
ou 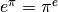 .
.
- 1
John Napier, ou Jean Neper en français, a vécu entre 1550 et 1617 et est considéré comme l’inventeur des logarithmes. Il a développé ceux-ci pour simplifier ses calculs d’astronomie.