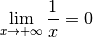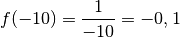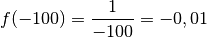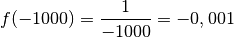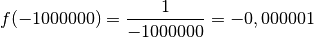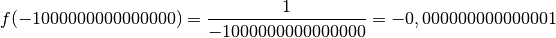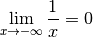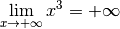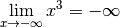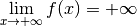3.6 Limites et divergence de fonctions en  et
et  ¶
¶
 en un point
en un point
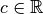 . Mais l’idée de limite (et de divergence)
peut également être déclinée pour parler du comportement
asymptotique d’une fonction, c’est-à-dire du comportement des
nombres
. Mais l’idée de limite (et de divergence)
peut également être déclinée pour parler du comportement
asymptotique d’une fonction, c’est-à-dire du comportement des
nombres 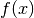 pour des valeurs de l’argument
pour des valeurs de l’argument  qui
deviennt de plus en plus grandes ou de plus en plus petites (grandes
négativement).
qui
deviennt de plus en plus grandes ou de plus en plus petites (grandes
négativement).Exemple 3.6.1. Nous souhaiterions pouvoir parler du comportement asymptotique de la fonction inverse, dont le graphe est pour rappel le suivant.
Nous aimerions savoir ce que deviennent les nombres 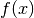 au fur
et à mesure que nous considérons des
au fur
et à mesure que nous considérons des  de plus en plus grands.
Voyons d’abord ce que vaut
de plus en plus grands.
Voyons d’abord ce que vaut 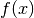 pour certaines valeurs de
pour certaines valeurs de
 particulières qui sont de plus en plus grandes :
particulières qui sont de plus en plus grandes :
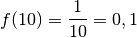
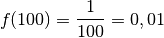
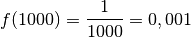
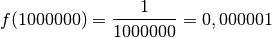

 par des nombres positifs
arbitrairement grands, le résultat sera un nombre positif
arbitrairement proche de
par des nombres positifs
arbitrairement grands, le résultat sera un nombre positif
arbitrairement proche de  . Au fur à mesure que les abscisses
. Au fur à mesure que les abscisses
 des points du graphes grandissent, les ordonnées
des points du graphes grandissent, les ordonnées
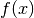 associées se rapprochent uniformément et définitivement
de
associées se rapprochent uniformément et définitivement
de  . Nous retrouvons l’idée de limite : la nouveauté étant
que nous observons le comportement de la fonction non pas à l’approche
d’un point, mais son comportement pour des nombres de plus en plus
grands.
. Nous retrouvons l’idée de limite : la nouveauté étant
que nous observons le comportement de la fonction non pas à l’approche
d’un point, mais son comportement pour des nombres de plus en plus
grands. quand
quand  tend vers
tend vers  . On note :
. On note : qui sont de plus en plus petites :
qui sont de plus en plus petites :
Plus généralement, si nous divisons
par des nombres négatifs arbitrairement petits, le résultat sera un nombre négatif arbitrairement proche de
. Au fur à mesure que les abscisses
des points du graphes diminuent, les ordonnées
associées se rapprochent uniformément et définitivement de
. Nous retrouvons une fois de plus l’idée de limite : la nouveauté étant que nous observons le comportement de la fonction non pas à l’approche d’un point, mais son comportement pour des nombres de plus en plus petits.
 quand
quand  tend vers
tend vers  . On note :
. On note :Remarque 3.6.2. Il se trouve que la fonction inverse a la même limite pour  tendant vers
tendant vers  et pour
et pour  tendant vers
tendant vers
 . Ce n’est bien évidemment pas toujours le cas. Par
exemple, la fonction dont le graphe est ci-dessous a comme limite
. Ce n’est bien évidemment pas toujours le cas. Par
exemple, la fonction dont le graphe est ci-dessous a comme limite
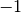 pour
pour  tendant vers
tendant vers  et
et  pour
pour
 tendant vers
tendant vers  .
.

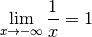
Donnons les définitions de limite d’une fonction pour  qui tend
vers
qui tend
vers  ou vers
ou vers  . Celle-ci est très
similaire à la définition de limite d’une fonction en un point et est
construite de la même manière.
. Celle-ci est très
similaire à la définition de limite d’une fonction en un point et est
construite de la même manière.
Définition 3.6.3. Soit un intervalle 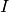 non majoré. Soit
non majoré. Soit  .
.
On dit que
a une limite
pour
qui tend vers
si pour toute marge d’erreur
, il existe
tel que pour tout
qui est plus grand ou égal à
, c’est-à-dire tel que
, on a nécessairement que
est à une distance plus petite ou égale de
que
, c’est-à-dire qu’on a
. Dans ce cas, on note :
Définition 3.6.4. Soit un intervalle 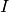 non minoré. Soit
non minoré. Soit  .
.
On dit que
a une limite
pour
qui tend vers
si pour toute marge d’erreur
, il existe
tel que pour tout
qui est plus petit ou égal à
, c’est-à-dire tel que
, on a nécessairement que
est à une distance plus petite ou égale de
que
, c’est-à-dire qu’on a
. Dans ce cas, on note :
Donnons quelques exemples et contre-exemples.
Exemple 3.6.5. La fonction dont le graphe est donné ci-dessous a comme limite 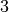 pour
pour  qui tend vers
qui tend vers  .
.
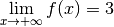
Pour cette fonction, il ne fait pas sens de parler d’une éventuelle
limite pour  qui tend vers
qui tend vers  puisque son domaine
de définition est
puisque son domaine
de définition est 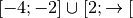 .
.
Exemple 3.6.6. La fonction dont le graphe est donné ci-dessous a comme limite
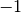 pour
pour  qui tend vers
qui tend vers  et pour
et pour
 qui tend vers
qui tend vers  .
.
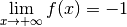
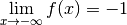
Contre-exemple 3.6.7. La fonction dont le graphe est donné ci-dessous n’a pas de limite pour
 qui tend vers
qui tend vers  et n’a pas de limite pour
et n’a pas de limite pour
 qui tend vers
qui tend vers  .
.
En effet, peu importe si on considère des nombres  de plus en
plus grands ou de plus en plus petits, les nombres
de plus en
plus grands ou de plus en plus petits, les nombres 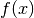 associées ne finiront jamais par se rapprocher de manière uniforme et
définitive d’une valeur unique. Ils continueront d’osciller autour de
associées ne finiront jamais par se rapprocher de manière uniforme et
définitive d’une valeur unique. Ils continueront d’osciller autour de
 encore et encore.
encore et encore.
Contre-exemple 3.6.8. La fonction dont le graphe est donné ci-dessous n’a pas de limite pour
 qui tend vers
qui tend vers  mais a comme limite
mais a comme limite  pour
pour  qui tend vers
qui tend vers  .
.
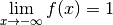
 qui tend vers
qui tend vers  ou pour
ou pour  qui tend
vers
qui tend
vers  , on peut parler de la divergence vers
, on peut parler de la divergence vers
 ou vers
ou vers  pour
pour  qui tend vers
qui tend vers
 ou pour
ou pour  qui tend vers
qui tend vers  . Une
fois de plus, introduisons cette nouvelle notion avec un exemple.
. Une
fois de plus, introduisons cette nouvelle notion avec un exemple.Exemple 3.6.9. Nous souhaiterions pouvoir parler du comportement asymptotique de la fonction cubique, dont le graphe est pour rappel le suivant.
Nous aimerions savoir ce que deviennent les nombres 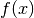 au fur
et à mesure que nous considérons des
au fur
et à mesure que nous considérons des  de plus en plus grands.
Voyons d’abord ce que vaut
de plus en plus grands.
Voyons d’abord ce que vaut 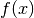 pour certaines valeurs de
pour certaines valeurs de
 particulières qui sont de plus en plus grandes :
particulières qui sont de plus en plus grandes :
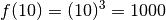
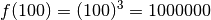

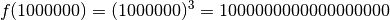
 des
points du graphes grandissent, les ordonnées
des
points du graphes grandissent, les ordonnées 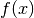 deviennent
uniformément et définitivement aussi grandes que l’on veut. Nous
retrouvons l’idée de divergence : la nouveauté étant que nous
observons le comportement de la fonction non pas à l’approche d’un
point, mais son comportement pour des nombres de plus en plus grands.
deviennent
uniformément et définitivement aussi grandes que l’on veut. Nous
retrouvons l’idée de divergence : la nouveauté étant que nous
observons le comportement de la fonction non pas à l’approche d’un
point, mais son comportement pour des nombres de plus en plus grands. quand
quand  tend vers
tend vers  . On note :
. On note : qui sont de plus en plus petites :
qui sont de plus en plus petites :
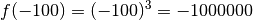
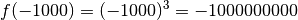
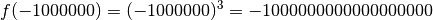
 des
points du graphes diminuent, les ordonnées
des
points du graphes diminuent, les ordonnées 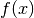 associées
deviennent uniformément et définitivement aussi petites que l’on veut.
Nous retrouvons une fois de plus l’idée de divergence : la nouveauté
étant que nous observons le comportement de la fonction non pas à
l’approche d’un point, mais son comportement pour des nombres de plus
en plus petits.
associées
deviennent uniformément et définitivement aussi petites que l’on veut.
Nous retrouvons une fois de plus l’idée de divergence : la nouveauté
étant que nous observons le comportement de la fonction non pas à
l’approche d’un point, mais son comportement pour des nombres de plus
en plus petits. quand
quand  tend vers
tend vers  . On note :
. On note : ou vers
ou vers
 d’une fonction pour
d’une fonction pour  qui tend vers
qui tend vers
 ou vers
ou vers  . Celle-ci est très similaire à
la définition de divergence d’une fonction en un point et est
construite de la même manière.
. Celle-ci est très similaire à
la définition de divergence d’une fonction en un point et est
construite de la même manière.Définition 3.6.10. Soit un intervalle 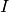 non majoré. Soit
non majoré. Soit  .
.
On dit que
a diverge vers
pour
qui tend vers
si pour toute borne supérieure
, il existe
tel que pour tout
qui est plus grand ou égal à
, c’est-à-dire tel que
, on a nécessairement que
est plus grand ou égal à
, c’est-à-dire qu’on a
. Dans ce cas, on note :
Définition 3.6.11. Soit un intervalle 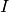 non majoré. Soit
non majoré. Soit  .
.
On dit que
a diverge vers
pour
qui tend vers
si pour toute borne inférieure
, il existe
tel que pour tout
qui est plus grand ou égal à
, c’est-à-dire tel que
, on a nécessairement que
est plus petit ou égal à
, c’est-à-dire qu’on a
. Dans ce cas, on note :
Définition 3.6.12. Soit un intervalle 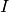 non minoré. Soit
non minoré. Soit  .
.
On dit que
a diverge vers
pour
qui tend vers
si pour toute borne supérieure
, il existe
tel que pour tout
qui est plus petit ou égal à
, c’est-à-dire tel que
, on a nécessairement que
est plus grand ou égal à
, c’est-à-dire qu’on a
. Dans ce cas, on note :
Définition 3.6.13. Soit un intervalle 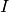 non majoré. Soit
non majoré. Soit  .
.
On dit que
a diverge vers
pour
qui tend vers
si pour toute borne inférieure
, il existe
tel que pour tout
qui est plus grand ou égal à
, c’est-à-dire tel que
, on a nécessairement que
est plus petit ou égal à
, c’est-à-dire qu’on a
. Dans ce cas, on note :
Donnons quelques exemples et contre-exemples.
Exemple 3.6.14. La fonction valeur absolue diverge vers  pour
pour  qui tend vers
qui tend vers  et diverge ves
et diverge ves  pour
pour
 qui tend vers
qui tend vers  .
.
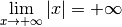
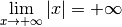
Exemple 3.6.15. La fonction racine carrée diverge vers  pour
pour  qui tend vers
qui tend vers  . Il ne fait pas sens de parler d’une
limite ou de divergence pour
. Il ne fait pas sens de parler d’une
limite ou de divergence pour  qui tend vers
qui tend vers  pour la racine carrée puisqu’elle n’est pas définie sur l’ensemble des
réels strictement négatifs.
pour la racine carrée puisqu’elle n’est pas définie sur l’ensemble des
réels strictement négatifs.
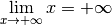
Exemple 3.6.16. La fonction dont le graphe est donné ci-dessous diverge vers
 pour
pour  qui tend vers
qui tend vers  et diverge
vers
et diverge
vers  pour
pour  qui tend vers
qui tend vers  .
.
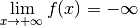
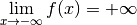
Contre-exemple 3.6.17. La fonction dont le graphe est donné ci-dessous ne diverge pas pour
 qui tend vers
qui tend vers  et ne diverge pas pour
et ne diverge pas pour  qui tend vers
qui tend vers  .
.
Contre-exemple 3.6.18. La fonction dont le graphe est donné ci-dessous diverge vers
 pour
pour  qui tend vers
qui tend vers  mais ne
diverge pas pour
mais ne
diverge pas pour  qui tend vers
qui tend vers  .
.
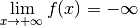
Remarque 3.6.19. Il existe une quantité non négligeable de résultats intéressants portant
sur les limites et les divergences de fonctions pour  qui tend
vers
qui tend
vers  ou vers
ou vers  . Néanmoins, dans ce cours,
nous nous contenterons d’utiliser ces notions comme des outils qui
permettent de décrire le comportement asymptotique d’une fonction.
. Néanmoins, dans ce cours,
nous nous contenterons d’utiliser ces notions comme des outils qui
permettent de décrire le comportement asymptotique d’une fonction.
Passons aux exercices.
Exercice 3.6.20. (Exercice théorique un peu difficile.)
Les définitions 3.6.3 et 3.6.4 sont très similaires. Identifier la seule petite différence et expliquer celle-ci.
Exercice 3.6.21. Tracer le graphe d’une fonction  ayant les propriétés suivantes
:
ayant les propriétés suivantes
:
Solution.
Exercice 3.6.22. Déterminer si les fonctions dont les graphes sont donnés ci-dessous
ont une limite ou divergent pour  qui tend vers
qui tend vers
 ou
ou  .
.








Exercice 3.6.23. Déterminer si les fonctions convergent ou divergent pour  qui
tend vers
qui
tend vers  ou pour
ou pour  qui tend vers
qui tend vers
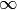 . Si elles convergent, donner la limite. Si elles
divergent, donner le type de divergence (vers
. Si elles convergent, donner la limite. Si elles
divergent, donner le type de divergence (vers  ou vers
ou vers
 ). N’hésitez pas à vous aider d’un graphe.
). N’hésitez pas à vous aider d’un graphe.






Exercice 3.6.24. Un homme souhaite changer la teneur en sel de son aquarium pour y accueillir de nouveaux poissons. Alors que son aquarium contient initialement 3 litres d’eau douce, il commence à remplir l’aquarium avec à la fois de l’eau douce et de l’eau salée (avec deux pompes différentes). La pompe d’eau douce a un débit d’un centilitre par seconde, tandis que la pompe d’eau salée a un débit de deux centilitres par seconde.
Quel est le rapport de la quantité d’eau douce et de la quantité d’eau salée après une minute de remplissage ?
Quel est le rapport de la quantité d’eau douce et de la quantité d’eau salée après
 secondes de remplissage ? (
secondes de remplissage ? (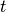 étant un nombre réel strictement positif quelconque.)
étant un nombre réel strictement positif quelconque.)Au fur et à mesure que le temps passe, de quoi se rapproche le rapport de la quantité d’eau douce et de la quantité d’eau salée ?

Exercice 3.6.25. Un avion a une panne de moteur en plein vol à une altitude de
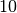 km et menace de s’écraser. Le pilote va essayer de faire
planer l’avion jusqu’au prochain aréoport, mais il craint que l’avion
perde trop d’altitude en planant.
km et menace de s’écraser. Le pilote va essayer de faire
planer l’avion jusqu’au prochain aréoport, mais il craint que l’avion
perde trop d’altitude en planant.
Il se souvient de ses cours d’aviation que dans ce genre de situation,
l’avion perd d’abord rapidement beaucoup d’altitude mais se stabilise
peu à peu. Il se souvient que dans ce genre de situation, l’altitude
de l’avion après 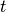 heures est de
heures est de 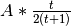 où
où
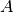 est l’altitude initiale de l’avion.
est l’altitude initiale de l’avion.
De quelle altitude se rapproche de l’avion au fur et à mesure que le temps passe ? Risque-t-il de s’écraser ?