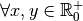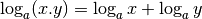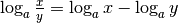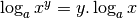Théorie¶
Les fonctions exponentielles et logarithmes¶
1. Définition¶
Soit 
un nombre 
.
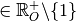- L’exponentielle de base
, ( 
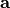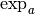) est une fonction de
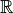dans 
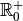qui à
chaque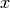 
fait correspondre une image notée 
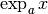ou
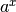qui se définit de la manière suivante:
si
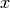est un rationnel, c-à-d qu’il s’écrit sous la forme
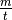avec 
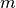et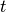 
entiers premiers entre
eux alors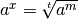 
.
On prolonge cette fonction sur 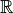de manière continue:
si
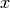est un irrationnel; il existe une suite de rationnels
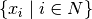telle que 
,
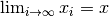alors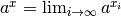 
Si un phénomène (par ex. une population) évolue de sorte que, sur des intervalles de temps égaux, il s’accroit dans la même proportion, on dira qu’il a une croissance exponentielle ; il peut s’exprimer au moyen d’une fonction exponentielle:
Appelons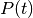 
la population au temps 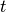. Si elle est
multipliée par 2 durant l’unité de temps, on a
.
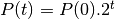De manière générale, si une quantité Q(t) évolue de manière
exponentielle et que le facteur multiplicatif par unité de temps est
a, on a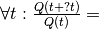 
constante, en particulier 
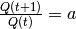, son équation est : 
.
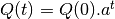Le logarithme de base a (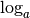 
) est la réciproque de la
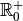fonction exponentielle ; c’est donc une fonction de dans 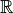qui à chaque
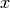fait correspondre un nombre 
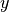noté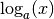 
tel que 
.
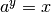Autrement dit, le logarithme en base d’un nombre est
l’exposant qu’il faut mettre à pour obtenir une puissance égale à ce nombre.
2. Propriétés du logarithme¶
Ces propriétés se démontrent en utilisant les propriétés des exposants.
