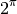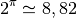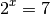Cours de mathématiques de sixième année
4 périodes/semaine
Année 2018-2019
Lycée Martin V
Les fonctions exponentielles et logarithmes sont très utiles dans de
nombreux contextes. Qu’on parle de radioactivité, de séisme, de
démographie, d’acidité d’une solution ou encore d’intensité du son,
elles constituent un outil essentiel pour étudier de nombreux
phénomènes.
Par ailleurs, ces fonctions ont également un intérêt mathématique
intrinsèque remarquable, en particulier la fonction exponentielle de
base  et le logarithme népérien. Nous découvrirons pourquoi
ainsi que l’identité de ce nombre
et le logarithme népérien. Nous découvrirons pourquoi
ainsi que l’identité de ce nombre  qui possède un statut
semblable à celui de
qui possède un statut
semblable à celui de 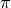 dans les mathématiques modernes.
dans les mathématiques modernes.
 et le logarithme népérien. Nous découvrirons pourquoi
ainsi que l’identité de ce nombre
et le logarithme népérien. Nous découvrirons pourquoi
ainsi que l’identité de ce nombre  qui possède un statut
semblable à celui de
qui possède un statut
semblable à celui de 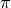 dans les mathématiques modernes.
dans les mathématiques modernes.Après avoir donné une courte introduction où seront présentées cinq
raisons différentes d’explorer ce nouveau chapitre, nous allons
découvrir la notion de fonction exponentielle en généralisant les
exposants que nous connaissons déjà : les exposants rationnels. Nous
définirons ensuite les fonctions logarithmes comme les fonctions
réciproques des fonctions exponentielles. Enfin, nous apprendrons à
exploiter ces nouveaux outils et nous reviendrons sur l’introduction.
Pour ce chapitre, les prérequis sont les suivants :
Puissances/exposants naturels, entiers et rationnels
Fonctions
Limites et continuité de fonctions
Dérivées
Intégrales
1 Introduction¶
1.1 Des exposants irrationnels ?¶
À ce stade, vous êtes déjà familier avec les exposants naturels
(non-nuls). Par exemple, vous savez certainement quel est le sens de
la notation  : il s’agit du nombre
: il s’agit du nombre 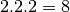 .
.
 : il s’agit du nombre
: il s’agit du nombre 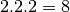 .
.Vous êtes également déjà familier avec les exposants entiers et en
particulier les exposants négatifs. Par exemple, vous savez
certainement quel est le sens de la notation 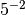 : il
s’agit du nombre
: il
s’agit du nombre  .
.
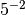 : il
s’agit du nombre
: il
s’agit du nombre  .
.Idéalement, vous êtes aussi familier avec les exposants rationnels.
Par exemple, vous devriez savoir quel est le sens de la notation
 : il s’agit du nombre
: il s’agit du nombre
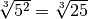 .
.
 : il s’agit du nombre
: il s’agit du nombre
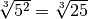 .
.Quid des exposants irrationnels ? Par exemple, la notation suivante
a-t-elle un sens ?
A priori, non. Non seulement
n’est pas un nombre rationnel, mais on voit mal comment on pourrait étendre le sens donné aux exposants (initialement) pour un exposant tel que
:
Pourtant, si on entre
dans une calculatrice, elle retourne une approximation de ce nombre :
Il doit donc sans doute être possible d’accorder à cette notation un sens univoque et de calculer ce nombre (ou au moins une approximation de ce nombre).
Dans ce chapitre, nous allons découvrir le sens que l’on peut
attribuer aux exposants irrationnels et nous essayerons de comprendre
comment une calculatrice peut nous retourner une telle valeur.
1.2 Des équations irrésolubles ?¶
Si on vous demande de trouver un nombre 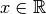 tel
que
tel
que 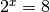 , vous répondrez sans aucune difficulté que
, vous répondrez sans aucune difficulté que
 est solution car
est solution car 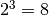 .
.
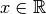 tel
que
tel
que 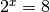 , vous répondrez sans aucune difficulté que
, vous répondrez sans aucune difficulté que
 est solution car
est solution car 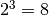 .
.De même, si on vous demande de trouver un nombre
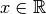 tel que
tel que  , vous répondrez sans
aucune difficulté que
, vous répondrez sans
aucune difficulté que  est solution car
est solution car  .
.
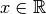 tel que
tel que  , vous répondrez sans
aucune difficulté que
, vous répondrez sans
aucune difficulté que  est solution car
est solution car  .
.À nouveau, si on vous demande de trouver un nombre
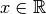 tel que
tel que  , vous
répondrez sans grande difficulté que
, vous
répondrez sans grande difficulté que  est solution car
est solution car
 .
.
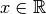 tel que
tel que  , vous
répondrez sans grande difficulté que
, vous
répondrez sans grande difficulté que  est solution car
est solution car
 .
.De manière générale, si le nombre  d’une
équation
d’une
équation 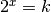 peut être exprimé comme une puissance entière
de
peut être exprimé comme une puissance entière
de 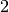 , il est facile de trouver une solution.
, il est facile de trouver une solution.
 d’une
équation
d’une
équation 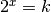 peut être exprimé comme une puissance entière
de
peut être exprimé comme une puissance entière
de 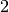 , il est facile de trouver une solution.
, il est facile de trouver une solution.Mais que se passe-t-il si le nombre  ne peut
pas être exprimé comme une puissance entière de
ne peut
pas être exprimé comme une puissance entière de 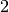 ? Par
exemple, comment trouver un nombre
? Par
exemple, comment trouver un nombre 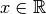 tel que :
tel que :
 ne peut
pas être exprimé comme une puissance entière de
ne peut
pas être exprimé comme une puissance entière de 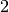 ? Par
exemple, comment trouver un nombre
? Par
exemple, comment trouver un nombre 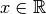 tel que :
tel que :
Si un tel nombre
existe (ce qui n’est a priori même pas certain), il s’agit sans doute d’un nombre entre
et
(puisque
et
) et sans doute un peu plus proche de
que de
. Mais cela ne nous avance pas beaucoup…
Dans ce chapitre, nous allons voir qu’un tel nombre existe bel et bien
et nous découvrirons les outils qui permettent de l’exprimer et de
résoudre une telle équation. Nous verrons que ce type d’équation peut
apparaître dans plusieurs contextes, dont un que vous avez normalement
déjà rencontré l’année passé : les intérêts composés.
1.3 Une primitive de la fonction inverse ?¶
Dans le chapitre des intégrales, nous nous sommes étonnés du fait que
la fonction inverse était l’unique fonction de référence pour laquelle
nous n’étions pas capable de trouver une primitive.
Néanmoins, puisque la fonction inverse est continue, le premier
théorème fondamental de l’analyse nous garantit son existence, au
moins sur un intervalle compact.
Dans ce chapitre, nous allons découvrir cette primitive et nous
verrons qu’il s’agit d’une fonction extrêmement importante qui a bien
d’autres propriétés essentielles que celle d’être une primitive de la
fonction inverse.
1.4 Une fonction qui est sa propre dérivée/primitive ?¶
Dans le cadre du chapitre des intégrales, une question qui peut
survenir assez naturellement est celle de l’existence d’une fonction
qui est sa propre dérivée ou (de façon équivalente) sa propre
primitive.
Dans ce chapitre, nous allons découvrir une telle fonction et nous
verrons qu’elle est unique ! De plus, nous apprendrons qu’il s’agit
d’une fonction extrêmement importante, voire fondamentale. Nous
verrons qu’elle possède de nombreuses propriétés très intéressantes et
qu’elle est extrêmement liée à la fameuse primitive de la fonction
inverse dont nous parlions dans la sous-section précédente.
1.5 Des échelles logarithmiques ?¶
Certaines unités de mesure peuvent être troublantes pour ceux qui ne
les comprennent pas. Un tremblement de terre d’une magnitude de
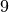 (un cataclysme historique, seulement 5 tremblements de terre
de cette ampleur ont été recencés dans le monde depuis 1900) n’est
certainement pas seulement
(un cataclysme historique, seulement 5 tremblements de terre
de cette ampleur ont été recencés dans le monde depuis 1900) n’est
certainement pas seulement 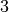 fois plus intense et destructeur
qu’un tremblement de terre d’une magnitude de
fois plus intense et destructeur
qu’un tremblement de terre d’une magnitude de 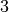 (en moyenne,
il y a plus d’un tremblement de terre de ce type en Belgique par an et
la plupart des gens l’ignorent). Un son d’une intensité de
(en moyenne,
il y a plus d’un tremblement de terre de ce type en Belgique par an et
la plupart des gens l’ignorent). Un son d’une intensité de 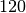 décibels (ce qui correspond environ à l’intensité du son d’une
vuvuzela proche) n’est certainement pas seulement
décibels (ce qui correspond environ à l’intensité du son d’une
vuvuzela proche) n’est certainement pas seulement 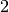 fois plus
fort qu’un son de
fois plus
fort qu’un son de  décibels (ce qui correspond environ à
l’intensité du son lors d’une discussion normale avec une personne
proche). Une solution dont le pH est de
décibels (ce qui correspond environ à
l’intensité du son lors d’une discussion normale avec une personne
proche). Une solution dont le pH est de 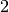 (plus ou moins
l’acidité de l’acide gastrique) n’est certainement pas seulement
(plus ou moins
l’acidité de l’acide gastrique) n’est certainement pas seulement
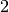 fois plus acide qu’une solution dont le pH est de
fois plus acide qu’une solution dont le pH est de  (plus ou moins l’acidité d’un vin).
(plus ou moins l’acidité d’un vin).
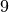 (un cataclysme historique, seulement 5 tremblements de terre
de cette ampleur ont été recencés dans le monde depuis 1900) n’est
certainement pas seulement
(un cataclysme historique, seulement 5 tremblements de terre
de cette ampleur ont été recencés dans le monde depuis 1900) n’est
certainement pas seulement 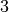 fois plus intense et destructeur
qu’un tremblement de terre d’une magnitude de
fois plus intense et destructeur
qu’un tremblement de terre d’une magnitude de 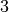 (en moyenne,
il y a plus d’un tremblement de terre de ce type en Belgique par an et
la plupart des gens l’ignorent). Un son d’une intensité de
(en moyenne,
il y a plus d’un tremblement de terre de ce type en Belgique par an et
la plupart des gens l’ignorent). Un son d’une intensité de 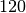 décibels (ce qui correspond environ à l’intensité du son d’une
vuvuzela proche) n’est certainement pas seulement
décibels (ce qui correspond environ à l’intensité du son d’une
vuvuzela proche) n’est certainement pas seulement 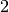 fois plus
fort qu’un son de
fois plus
fort qu’un son de  décibels (ce qui correspond environ à
l’intensité du son lors d’une discussion normale avec une personne
proche). Une solution dont le pH est de
décibels (ce qui correspond environ à
l’intensité du son lors d’une discussion normale avec une personne
proche). Une solution dont le pH est de 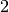 (plus ou moins
l’acidité de l’acide gastrique) n’est certainement pas seulement
(plus ou moins
l’acidité de l’acide gastrique) n’est certainement pas seulement
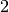 fois plus acide qu’une solution dont le pH est de
fois plus acide qu’une solution dont le pH est de  (plus ou moins l’acidité d’un vin).
(plus ou moins l’acidité d’un vin).Il se trouve que toutes ces unités cachent en fait une échelle
logarithmique. Pour comprendre ces échelles et ces unités, il est
essentiel de comprendre la notion à partir de laquelle elles sont
construites : les fonctions logarithmes.
Dans ce chapitre, nous allons non seulement découvrir ces fonctions
logarithmes, mais nous intéresserons également dans la dernière
section du chapitre à la façon dont elles permettent de parler
d’échelles logarithmiques.