2.3 Propriétés des fonctions continues¶
Commençons avec un exemple :
Exemple 2.3.1. Considérons les deux fonctions :
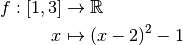
et
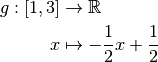
dont les graphes sont les suivants :
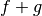 ? Au niveau des graphes, cela
revient à additionner les ordonnées des points des graphes de
? Au niveau des graphes, cela
revient à additionner les ordonnées des points des graphes de
 et
et 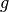 qui ont la même abscisse.
qui ont la même abscisse.Sans surprise, aucune discontinuité n’est apparue. En additionnant deux fonctions continues, on a obtenu une nouvelle fonction continue. Ce n’est pas un hasard, comme l’indique la proposition suivante.
Proposition 2.3.2. Soit 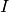 un intervalle éventuellement privé d’un point. Soient
un intervalle éventuellement privé d’un point. Soient
 et
et 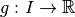 deux
fonctions continues. Alors :
deux
fonctions continues. Alors :
La fonction
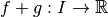 est continue.
est continue.La fonction
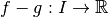 est continue.
est continue.La fonction
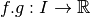 est continue.
est continue.La fonction
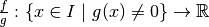 est
continue.
est
continue.
Démonstration Pas en math 4. Voir annexe pour les curieux.
De manière éventuellement plus surprenante, la composée de deux fonctions continues (compatibles) est également toujours une fonction continue :
Proposition 2.3.3. Soit 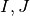 deux intervalles. Soient
deux intervalles. Soient
 et
et 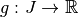 deux
fonctions continues telle que
deux
fonctions continues telle que
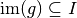 . Alors :
. Alors :
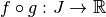 est continue.
est continue.
Démonstration Pas en math 4.
Une dernière opération qui conserve la continuité est la restriction :
Définition 2.3.4. Soit 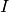 un intervalle éventuellement privé d’un point. Soit
un intervalle éventuellement privé d’un point. Soit
 .
Soit
.
Soit 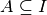 . Alors la restriction de
. Alors la restriction de  sur
sur
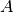 est la fonction :
est la fonction :
Exemple 2.3.5. Soit la fonction :
dont le graphe est :
La restriction de  sur, par exemple,
sur, par exemple,
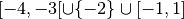 , est la fonction :
, est la fonction :
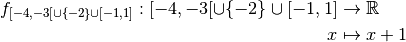
et son graphe est :
Comme annoncé, la restriction d’une fonction continue est toujours continue :
Proposition 2.3.6. Soit 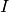 un intervalle éventuellement privé d’un point.
Soit
un intervalle éventuellement privé d’un point.
Soit  une fonction continue. Soit
une fonction continue. Soit
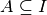 .
Alors la restriction de
.
Alors la restriction de  sur
sur 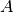 est continue.
est continue.
Démonstration Pas en math 4. Notons néanmoins que la démonstration est extrêment simple.
Grâce au théorème 2.2.1, nous savons que toutes les fonctions de référence sont continues. Or, les propositions 2.3.2, 2.3.3 et 2.3.6 nous disent que lorsqu’on combine deux fonctions continues selon une des opérations sur les fonctions les plus simples, nous pouvons être certains que le résultat est lui aussi une fonction continue. Ainsi, nous sommes à présent capables de justifier la continuité de nombreuses fonctions.
Exercice 2.3.7. Les fonctions suivantes sont-elles continues ? Si oui, justifier. Si non, faire le graphe de la fonction et donner l’ensemble des points de discontinuité.