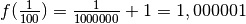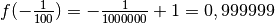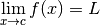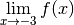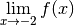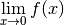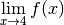3 Limites de fonctions¶
3.1 Définition et exemples¶
Pour découvrir la notion de limite qui est la formalisation de l’idée intuitive se rapprocher de (de façon définitive et uniforme) , commençons avec un exemple :
Définition 3.1.1. Soit la fonction

Son graphe est le suivant :
Au fur et à mesure que la variable  se rapproche de
se rapproche de  ,
de quelle valeur se rapproche
,
de quelle valeur se rapproche 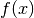 ? Pour nous aider à y voir
plus clair, évaluons la fonction
? Pour nous aider à y voir
plus clair, évaluons la fonction  en plusieurs nombres qui se
rapprochent de
en plusieurs nombres qui se
rapprochent de  :
:
 se rapproche de
se rapproche de  , plus
, plus
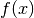 se rapproche de
se rapproche de  et ce de manière uniforme et
définitive : non seulement on se rapproche de cette valeur
et ce de manière uniforme et
définitive : non seulement on se rapproche de cette valeur  aussi bien par la droite que par la gauche , mais ce rapprochement se
fait autant que possible (sans pour autant que la fonction ne prenne
jamais la valeur
aussi bien par la droite que par la gauche , mais ce rapprochement se
fait autant que possible (sans pour autant que la fonction ne prenne
jamais la valeur  ) : les valeurs de
) : les valeurs de 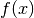 se
rapprochent autant qu’on le souhaite de la valeur
se
rapprochent autant qu’on le souhaite de la valeur  à
condition que les valeurs de
à
condition que les valeurs de  soient assez proches de
soient assez proches de
 .
. se rapproche bien de
se rapproche bien de  quand les
quand les  se rapprochent de
se rapprochent de  : si on se fixe une
certaine marge d’erreur autour de
: si on se fixe une
certaine marge d’erreur autour de  (par exemple une marge
d’erreur de
(par exemple une marge
d’erreur de  ), les valeurs de la fonction
), les valeurs de la fonction
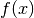 ne s’éloignent pas de
ne s’éloignent pas de  d’une distance supérieure
à l’erreur fixée à condition que les
d’une distance supérieure
à l’erreur fixée à condition que les  choisis soient assez
proches de
choisis soient assez
proches de  (avec une marge d’erreur de
(avec une marge d’erreur de
 , les
, les  disponibles sont ceux ne
s’éloignant pas de
disponibles sont ceux ne
s’éloignant pas de  de plus de
de plus de 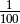 ).
Si la
fonction
).
Si la
fonction  se rapproche bien de
se rapproche bien de  quand les
quand les  se rapprochent de
se rapprochent de  , alors ce test devrait fonctionner quel
que soit la marge d’erreur (non nulle) qu’on s’est donnée, même si
celle-ci est extrêmement petite. Cette idée relativement naturelle
mais complexe est en fait la définition rigoureuse de la notion de
limite.
, alors ce test devrait fonctionner quel
que soit la marge d’erreur (non nulle) qu’on s’est donnée, même si
celle-ci est extrêmement petite. Cette idée relativement naturelle
mais complexe est en fait la définition rigoureuse de la notion de
limite.Définition 3.1.2. Soit un intervalle 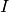 éventuellement privé d’un point
éventuellement privé d’un point  . Soit
. Soit  .
.
On dit que
a une limite
en
si pour toute marge d’erreur
, il existe
tel que pour tout
qui est à une distance plus petite ou égale de
que
, c’est-à-dire tel que
, on a nécessairement que
est à une distance plus petite ou égale de
que
, c’est-à-dire qu’on a
. Dans ce cas, on note :
Exemple 3.1.3. La fonction

a comme limite  en
en  . On note :
. On note :
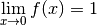
Remarque 3.1.4. Notons que dans l’exemple ci-dessus, la fonction  possède une
limite en
possède une
limite en  qui vaut
qui vaut  mais est également définie en
mais est également définie en
 de telle sorte que
de telle sorte que 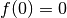 . Il est important de
comprendre qu’une limite d’une fonction en un point (si elle existe)
n’est pas toujours égale à la valeur de la fonction en ce point (la
fonction peut même ne pas être définie en ce point). C’est d’ailleurs
tout l’intérêt de la notion de limite : elle permet de parler d’une
valeur de laquelle se rapproche une fonction en un point sans que cette
fonction ne soit jamais égale à cette valeur.
. Il est important de
comprendre qu’une limite d’une fonction en un point (si elle existe)
n’est pas toujours égale à la valeur de la fonction en ce point (la
fonction peut même ne pas être définie en ce point). C’est d’ailleurs
tout l’intérêt de la notion de limite : elle permet de parler d’une
valeur de laquelle se rapproche une fonction en un point sans que cette
fonction ne soit jamais égale à cette valeur.
Voici à présent un théorème important mais que nous ne pourrons malheureusement pas démontrer :
Théorème 3.1.5. Soit un intervalle 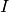 éventuellement privé d’un point
éventuellement privé d’un point
 . Soit
. Soit  .
Si
.
Si  possède une limite en
possède une limite en  , alors cette limite est
unique.
, alors cette limite est
unique.
Il fait donc sens de parler de LA limite d’une fonction en un point. Ce théorème ne devrait pas vous surprendre : si on se rapproche de manière uniforme et définitive d’un endroit, on ne peut pas en même temps se rapprocher de manière uniforme et définitive d’un autre endroit.
Exemple 3.1.6. Soit la fonction carrée, dont le graphe est :
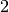 et cette limite vaut
et cette limite vaut
 :
: 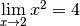 .
. .
.Exemple 3.1.7. Soit la fonction dont le graphe est :
Cette fonction ne possède pas de limite en 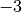 : quand les
: quand les
 se rapprochent de
se rapprochent de 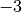 , les
, les 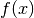 ne se
rapprochent pas uniformément d’un unique nombre (ils se rapproche de
ne se
rapprochent pas uniformément d’un unique nombre (ils se rapproche de
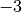 par la gauche et de
par la gauche et de 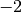 par la droite ).
par la droite ).
Exemple 3.1.8. Soit la fonction dont le graphe est :
La fonction n’est pas définie en  mais elle possède néanmoins
une limite en
mais elle possède néanmoins
une limite en  : quand les
: quand les  se rapprochent de
se rapprochent de
 , les
, les 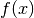 se rapprochent uniformément et
définitivement de
se rapprochent uniformément et
définitivement de 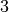 . On note :
. On note :
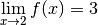
Définition 3.1.9. Soit la fonction dont le graphe est :
La fonction n’est pas définie en  mais elle possède néanmoins
une limite en
mais elle possède néanmoins
une limite en  : quand les
: quand les  se rapprochent de
se rapprochent de
 , les
, les 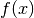 se rapprochent uniformément et
définitivement de
se rapprochent uniformément et
définitivement de 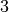 . On note :
. On note :
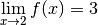
Exercice 3.1.10. À l’aide d’un graphique, déterminer si les limites suivantes existent. Si oui, donner les valeurs de celles-ci.




Exercice 3.1.11. Voici le graphe de la fonction  . Déterminer si les limites
suivantes existent. Si oui, donner les valeurs de celles-ci.
. Déterminer si les limites
suivantes existent. Si oui, donner les valeurs de celles-ci.

Exercice 3.1.12. Tracer le graphe d’une fonction  définie sur
définie sur
 qui n’a pas de limite en
qui n’a pas de limite en
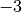 et qui a une limite en
et qui a une limite en  qui vaut
qui vaut 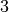 .
.
Solution.
Exercice 3.1.13. Déterminer si les limites suivantes si elles existent.










Exercice 3.1.14. Tracer le graphe d’une fonction  ayant les propriétés suivantes
:
ayant les propriétés suivantes
:
dom

 est continue partout sauf en
est continue partout sauf en 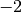 .
. n’a pas de limite en
n’a pas de limite en 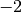 et en
et en 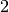
 a une limite en
a une limite en 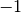 qui vaut
qui vaut 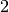 et une limite
en
et une limite
en  qui vaut
qui vaut 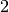
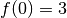 et
et 
 a exactement deux racines et elles se trouvent entre
a exactement deux racines et elles se trouvent entre
 et
et 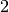 .
.
Solution.