2.5 Prolongements continus¶
Exemple 2.5.1. Voici le graphe d’une fonction définie sur
 qui est continue :
qui est continue :
Il ne fait pas sens de dire qu’elle est discontinue (ou continue) en
 puisqu’elle n’est pas définie en
puisqu’elle n’est pas définie en  .
.
Exemple 2.5.2. Voici le graphe d’une autre fonction définie sur
 qui est continue :
qui est continue :
Il ne fait pas sens de dire qu’elle est continue (ou discontinue) en
 puisqu’elle n’est pas définie en
puisqu’elle n’est pas définie en  .
.
 de sorte que le résultat final soit continu,
même en
de sorte que le résultat final soit continu,
même en  . Par contre, pour la deuxième fonction, il est
possible de trouver un tel prolongement continu : il suffit d’étendre
la fonction en la définissant en
. Par contre, pour la deuxième fonction, il est
possible de trouver un tel prolongement continu : il suffit d’étendre
la fonction en la définissant en  en décidant que le
prolongement de la fonction vaut
en décidant que le
prolongement de la fonction vaut 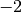 en
en  . Cette
intuition correspond au fait que la deuxième fonction possède un
prolongement continu tandis que la première non.
. Cette
intuition correspond au fait que la deuxième fonction possède un
prolongement continu tandis que la première non.Définition 2.5.3. Soit un intervalle 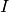 et soit
et soit 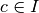 . Soit
. Soit 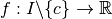 .
.
Un prolongement continu de
sur
est une fonction
qui est continue (y compris en
) et telle que pour tout
, on a
.
Exemple 2.5.4. La fonction de l’exemple 2.5.1 ne possède pas de prolongement continu. Par contre, la fonction de l’exemple 2.5.2 possède un prolongement continu dont le graphe est le suivant :
Dans le cas de cet exemple, puisque nous possédions déjà le graphe de la fonction, ce prolongement continu n’était pas très difficile à trouver.
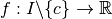 (où
(où 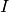 est un
intervalle et
est un
intervalle et 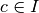 ) donnée, cette fonction admet un
prologement continu ? Intuitivement, il n’est pas très difficle de
répondre à cette question : il faut que la fonction
) donnée, cette fonction admet un
prologement continu ? Intuitivement, il n’est pas très difficle de
répondre à cette question : il faut que la fonction  se
rapproche d’une certaine valeur lorsqu’on se rapproche de
se
rapproche d’une certaine valeur lorsqu’on se rapproche de  ,
et ce de manière uniforme (il faut que la valeur de laquelle
,
et ce de manière uniforme (il faut que la valeur de laquelle  se rapproche par la gauche soit la même que celle de laquelle
se rapproche par la gauche soit la même que celle de laquelle
 se rapproche par la droite ). Néanmoins, cette réponse
intuitive soulève au moins trois questions.
se rapproche par la droite ). Néanmoins, cette réponse
intuitive soulève au moins trois questions.Que signifie rigoureusement que la fonction
 se rapproche
d’une valeur lorsqu’on se rapproche de
se rapproche
d’une valeur lorsqu’on se rapproche de  ?
?Comment savoir si la fonction
 se rapproche bien d’une
certaine valeur de manière uniforme et définitive lorsqu’on se
rapproche de
se rapproche bien d’une
certaine valeur de manière uniforme et définitive lorsqu’on se
rapproche de  ?
?Si
 se rapproche bien d’une certaine valeur de manière
uniforme et définitive lorsqu’on se rapproche de
se rapproche bien d’une certaine valeur de manière
uniforme et définitive lorsqu’on se rapproche de  , comment
calculer cette valeur ?
, comment
calculer cette valeur ?
Pour répondre à ces questions, nous avons besoin d’une nouvelle notion : celle de limite de fonction.
- 1
Remarque : pour la plupart des fonctions de référence, la démonstration n’est pas très compliquée. N’hésitez pas à essayer de faire vous-même la preuve par exemple pour une fonction constante ou pour la fonction identité.
- 2
La démonstration de ce théorème est en fait assez compliquée et nécessite de bien comprendre les propriétés fondamentales des nombres réels. Heureusement, son énoncé est très intuitif.
- 3
La démonstration de ce théorème est aussi assez compliquée.